고정 헤더 영역
상세 컨텐츠
본문
멋쟁이사자처럼 X K-DIGITAL Training - 06.30
[참고] 2021.07.01 - [python/k-digital] - [K-DIGITAL] 머신러닝 알고리즘(4) KNN, K-MEANS, PCA
[K-DIGITAL] 머신러닝 알고리즘(4) KNN, K-MEANS, PCA
멋쟁이사자처럼 X K-DIGITAL Training - 06.30 KNN 알고리즘 (K-Nearest Neighbor Algorithm, K-최근접이웃알고리즘) 분류나 회귀에 사용되는 지도학습 알고리즘 새로운 데이터를 입력 받았을 때 K개의 근접한 데..
juran-devblog.tistory.com
KNN(K-Nearest Neighbor) 알고리즘
라이브러리
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasetssklearn.neighbors 사이킷런 KNN 알고리즘
sklearn.datasets 사이킷런이 기본으로 제공하는 데이터셋
데이터 준비
iris = datasets.load_iris()
* Iris Datasets (붓꽃 품종 분류 데이터)
- 주어지는 붓꽃 데이터 feature (X) : 꽃잎의 길이와 너비, 꽃받침의 길이와 너비

- 타겟 데이터 (Y) : 각 X에 대응되는 붓꽃의 품종

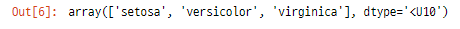
KNN 분석 적용
model = neighbors.KNeighborsClassifier(6) # n_neighbors=6- n_neighbors=6 가까운 이웃의 수(k)로 6 설정
모델 학습
model.fit(x, y)
모델 테스트
pred_data = model.predict(x, y)
* 모델 예측 시 행의 수보다 열의 수가 일치하는 것이 중요
예) (꽃받침의 길이, 꽃받침의 넓이) 형태로 X 데이터가 주어질 때 속한 클래스 y 반환
model.predict([[9, 2.5], [3.5, 11]])>> array([2, 0])
- 꽃받침의 길이가 9, 넓이가 3.5일때 class 2일것으로 예상
- 꽃받침의 길이가 2.5, 넓이가 11일때 class 0일것으로 예상
모델 시각화
- 꽃받침 길이(x축)와 넓이(y)에 따른 데이터 분포
# 열의 수를 맞춰주기위해 하나의 np.ndarray 형태로 변경
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# meshgrid(x, y, z) : x, y, z로 정의되는 3차원 그리드 좌표 반환
model.predict(np.c_[xx.ravel(), yy.ravel()])
plt.figure(figsize=(10,5))
plt.scatter(x[:, 0], x[:, 1])
plt.title("Data points")
plt.show()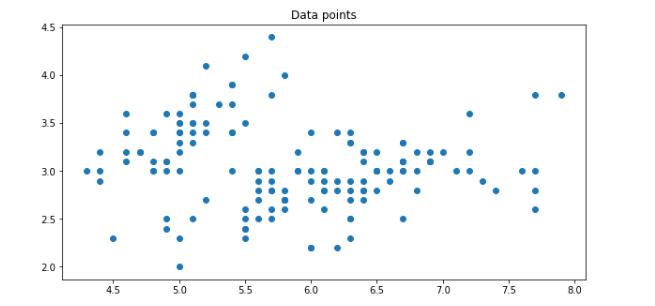
- n_neighbor=1일때 분류 결과
model = neighbors.KNeighborsClassifier(1)
model.fit(x, y)
# 전체 데이터 좌표 크기 계산
x_min, x_max = x[:,0].min() - 1, x[:,0].max() + 1
y_min, y_max = x[:,1].min() - 1, x[:,1].max() + 1
# 좌표 순서쌍
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# xy 좌표계 상의 각각의 Point에 대하여 KNN model class prediction 진행
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape) # xx.shape == (220, 280)
print(Z)
print(np.c_[xx.ravel(), yy.ravel()])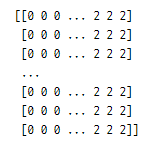

# 색 지정
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA','#00AAFF']) # x & y 좌표계 각 포인트
cmap_bold = ListedColormap(['#FF0000', '#00FF00','#0000FF']) # 실제 데이터
# cluster predict 결과
plt.figure(figsize=(10,5))
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=cmap_bold, edgecolors='gray')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = 1)")
plt.show()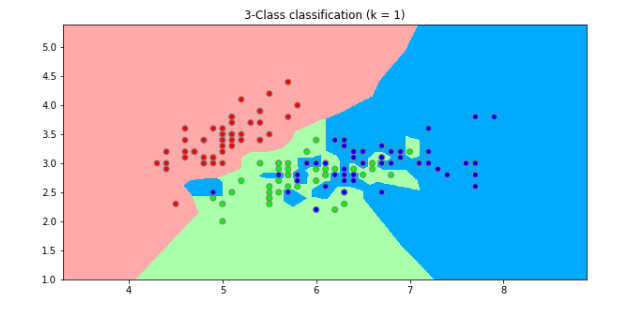
- n_neighbor=30일 때
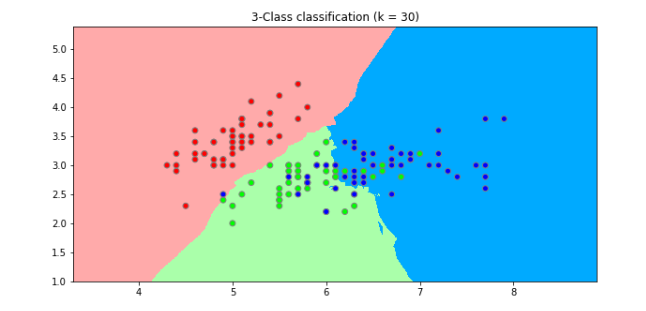
[참고] numpy.ndarray 차원간 변경 https://rfriend.tistory.com/349
[Python NumPy] 다차원 배열을 1차원 배열로 평평하게 펴주는 ravel(), flatten() 함수
이번 포스팅에서는 파이썬에서 다차원 배열(array)을 1차원 배열로 평평하게 펴주는 NumPy의 ravel() 함수, flatten() 함수에 대해서 알아보겠습니다. 1차원 배열을 다차원 배열로 재구성/재배열 해주는
rfriend.tistory.com
K-Means (K-평균) 알고리즘
라이브러리 추가
from mpl_toolkits.mplot3d import Axes3D # matplotlib 3차원 도구
from sklearn import metrics # 실루엣 계산
데이터 준비
- Iris dataset 이용
모델 학습
from sklearn import cluster
kmeans = cluster.KMeans(n_clusters=8).fit(X)
군집화 결과
kmeans.labels_>> [0 7 7 7 0 0 7 0 7 7 0 7 7 7 0 0 0 0 0 0]
중심값
kmeans.cluster_centers_
예측
kmeans.predict([[0, 0], [8, 4]])>> [0 1]
여러 모델 생성
estimators = [('k=8', cluster.KMeans(n_clusters=8)), # 클러스터 수 8
('k=3', cluster.KMeans(n_clusters=3)), # 클러스터 수 3
('k=3(r)', cluster.KMeans(n_clusters=3, n_init=1, init='random'))] # center - random init
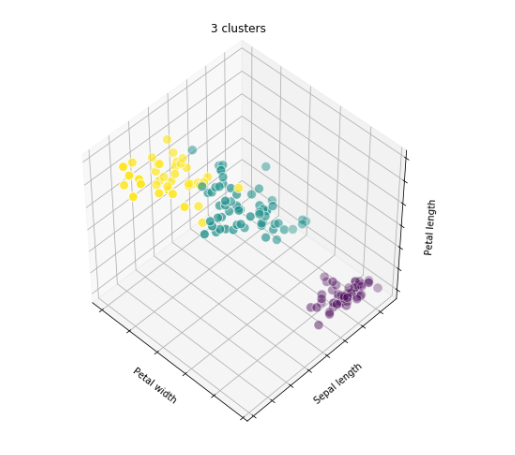
모델 시각화
fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']
for name, est in estimators:
fig = plt.figure(fignum, figsize=(7, 7))
# 3차원으로 바꿔줌
ax = Axes3D(fig, elev=48, azim=134) # 고도, 방위각
est.fit(X)
labels = est.labels_ # 클러스터랑 결과
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=labels.astype(np.float), edgecolor='w', s=100)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title(titles[fignum - 1])
ax.dist = 12
fignum = fignum + 1
plt.show()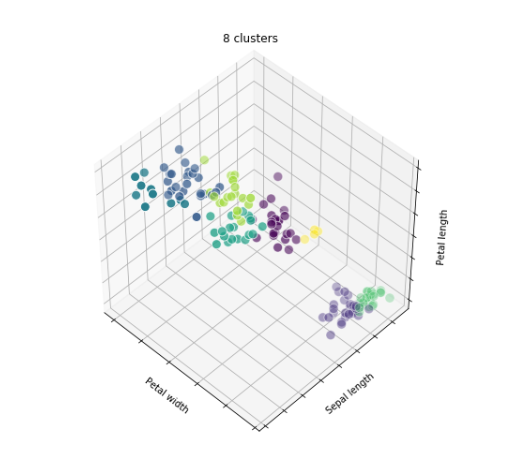
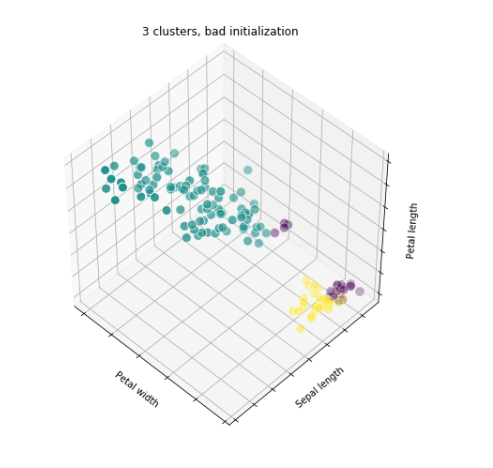
3 clusters, bad initialization
- 초기 센터값을 랜덤으로 설정
- 랜덤으로 선택된 값들이 한 cluster에 몰린 경우 제대로 클러스터링이 되지 않음
→ 최초 중심값 설정을 위한 알고리즘 k-means++ 를 기본으로 사용
클러스터 라벨 추가
fig = plt.figure(figsize=(7, 7))
ax = Axes3D(fig, elev=48, azim=134)
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(), X[y == label, 0].mean(), X[y == label, 2].mean()+2,
name, horizontalalignment='center')
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='w', s=100)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title('Ground Truth')
ax.dist = 12
plt.show()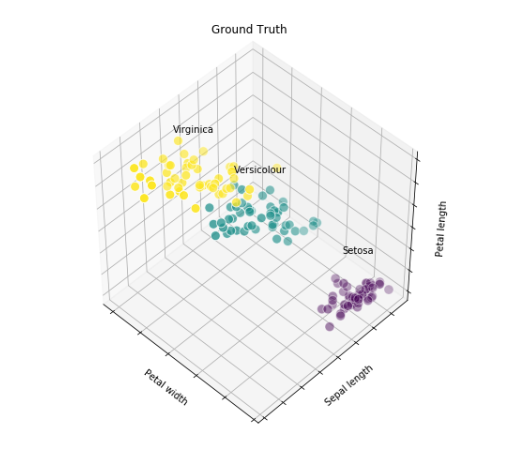
▷ 최적의 클러스터 개수 찾기
[전제 조건] 클러스터링을 마친 후 클러스터 내부에서는 뭉쳐있어야하고 다른 클러스터끼리는 떨어져있어야 한다.
1) 엘보우(elbow) 기법
SSE(Sum of Squered Errors)의 값이 점점 줄어들다가 어느 순간 줄어든느 비율이 급격하게 작아지는 부분 선택
그래프 모양에서 팔꿈치에 해당하는 부분(inertia가 꺾이는 지점)이 바로 최적의 클러스터 수
완벽한 지표 비교가 아니라 눈으로 선택하기 때문에 객관성이 다소 떨어짐
- inertia : 각 x마다 가장 가까운(소속된) 클러스터 센터와의 거리 제곱들의 합, k-means 클러스터링으로 계산된 SSE 값
def elbow(X):
total_distance = []
for i in range(1, 11): # i: 클러스터 수, 1~10
model = cluster.KMeans(n_clusters=i, random_state=0)
model.fit(X)
print(model.inertia_)
total_distance.append(model.inertia_)
plt.plot(range(1, 11), total_distance, marker='o')
plt.xlabel('# of clusters')
plt.ylabel('Total distance (SSE)')
plt.show()
elbow(X) 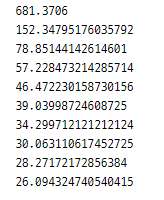
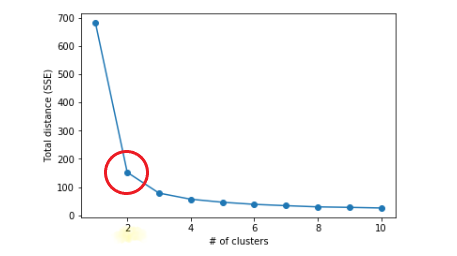
2) 실루엣(silhouette) 기법
클러스터링의 품질을 정량적으로 계산해주는 방법으로 모든 클러스터링 기법에 적용 가능
클러스터링이 끝난 후 데이터 1건마다 실루엣 계산
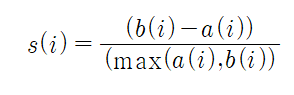
- 응집도(a): 동일한 클러스터 내의 나머지 데이터들과의 평균거리 / 낮을수록 좋음
- 분리도(b): 다른 클러스터 내의 모든 데이터들과의 평균거리 / 높을수록 좋음
→ 실루엣의 이상값은 1이며 1에 가까울수록 좋음
실루엣 계수 추이
import numpy as np
from sklearn.metrics import silhouette_samples
from matplotlib import cm
def plotSilhouette(X, y_fitted):
cluster_labels = np.unique(y_fitted)
n_clusters = cluster_labels.shape[0] # ex) (3,) -> 3
silhouette_vals = silhouette_samples(X, y_fitted, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for index, label in enumerate(cluster_labels):
cluster_silhouette_vals = silhouette_vals[y_fitted == label]
cluster_silhouette_vals.sort()
y_ax_upper += len(cluster_silhouette_vals)
plt.barh(range(y_ax_lower, y_ax_upper), cluster_silhouette_vals, height=1.0) # barh(y, data), edge_color=None
yticks.append((y_ax_lower + y_ax_upper) / 2)
y_ax_lower += len(cluster_silhouette_vals)
# 평균(빨간색)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color='red', linestyle='--')
print('The average silhouette value is', round(silhouette_avg, 2), '(near 0.7 or 0.7+ : desirable)')
plt.yticks(yticks, cluster_labels+1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette value')
plt.show()
model = cluster.KMeans(n_clusters=2)
y_fitted = model.fit_predict(X)
plotSilhouette(X, y_fitted)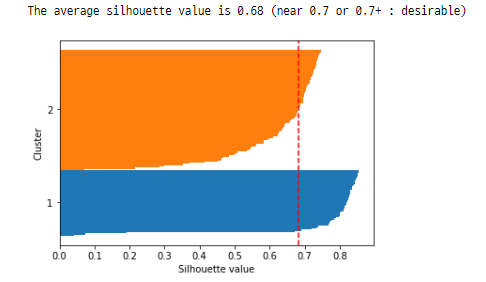
클러스터 수에 따른 실루엣 계수 확인
from sklearn.metrics import silhouette_score
# 클러스터 2개인 경우
model = cluster.KMeans(n_clusters=2)
y_fitted = model.fit_predict(X)
silhouette_avg = silhouette_score(X, y_fitted)
print("The average of silhouette coefficients is :", silhouette_avg)>> The average of silhouette coefficients is : 0.681046169211746
'PYTHON > K-DIGITAL' 카테고리의 다른 글
| [K-DIGITAL] 세미프로젝트2. 타이타닉 생존자 예측 모델 만들기(1) (0) | 2021.07.05 |
|---|---|
| [K-DIGITAL] 머신러닝 알고리즘(5) 스태킹 앙상블(Stacking Ensemble), vecstack 실습 (0) | 2021.07.01 |
| [K-DIGITAL] 머신러닝 알고리즘(4) KNN, K-MEANS, PCA (0) | 2021.07.01 |
| [K-DIGITAL] 분류 성능에 대한 측정 ROC Curve와 AUC (0) | 2021.07.01 |
| [K-DIGITAL] 머신러닝 알고리즘(3) 의사결정트리 - sklearn 실습 (0) | 2021.06.30 |
댓글 영역