고정 헤더 영역
상세 컨텐츠
본문
멋쟁이사자처럼 X K-DIGITAL Training - 06.29
[참고] 2021.06.30 - [python/k-digital] - [K-DIGITAL] 머신러닝 알고리즘(2) SVM
[K-DIGITAL] 머신러닝 알고리즘(2) SVM
멋쟁이사자처럼 X K-DIGITAL Training - 06.29 [이전] 2021.06.29 - [python/k-digital] - [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석과 분류분석 [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석과 분류분석 멋쟁이..
juran-devblog.tistory.com
라이브러리
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from library import custom_mglearn # library / custom_mglearn
from sklearn.datasets import make_blobs
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.svm import SVCsklearn.datasets.* 사이킷런에서 기본 제공되는 데이터셋 이용 가능
sklearn.model_selection.train_test_split 학습 데이터, 테스트 데이터 쉽게 분리
sklearn.svm.LinearSVC Linear Support Vector Classfier
sklearn.svm.SVC Support Vector Classifier
실습1) Sklearn 라이브러리 가상 데이터
데이터 준비 및 전처리
X, y = make_blobs(centers=4, random_state=8)
y = y % 2 # label 0,1,2,3 -> label 0,1모델 생성 후 학습
linear_svm = LinearSVC().fit(X, y)모델 시각화 (2차원)
- 직선 형태의 결정 경계 나타남
custom_mglearn.plot_2d_separator(linear_svm, X) # Plot the linear decision boundary
custom_mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
새로운 feature 추가하여 고차원으로 바꿔줌 (2차원 -> 3차원)
- 두번째 열 제곱하여 새로운 열로 추가
X_new = np.hstack([X, X[:, 1:] ** 2]) # X[:, 1:] 두번째 열- 데이터 시각화
from mpl_toolkits.mplot3d import Axes3D, axes3d # 3차원 그래프
figure = plt.figure()
# 3차원 그래프 생성
ax = Axes3D(figure, elev=-152, azim=-26)
# slicing
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=ListedColormap(['#0000aa', '#ff2020']), s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
cmap=ListedColormap(['#0000aa', '#ff2020']), s=60, edgecolor='k')
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_zlabel("Feature 1 ** 2")
plt.show()
3차원의 데이터로 모델 학습
linear_svm_3d = LinearSVC().fit(X_new, y)모델 시각화 (3차원)
- 3차원상에서 평면 형태의 결정 경계 그려짐
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
# 좌표계 생성
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xx, yy)
# 선형 결정 경계
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=ListedColormap(['#0000aa', '#ff2020']), s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
cmap=ListedColormap(['#0000aa', '#ff2020']), s=60, edgecolor='k')
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_zlabel("Feature 1 ** 2")
plt.show()
결정 경계 그린 후 기존의 좌표계로 복귀 (3차원 -> 2차원)
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
cmap=ListedColormap(['#0000aa', '#ff2020']), alpha=0.5)
custom_mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
▷ Kernel Function (고차원 mapping) 이용한 모델 학습
* 자주 사용되는 kernel function
- 다항식 커널 (polynomial kernel)
- 가우시안 커널 (rbf, radial basis function)
가우시안 커널
X, y = custom_mglearn.make_handcrafted_dataset()
# kernel function = 'rbf'
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y) 모델 시각화
custom_mglearn.plot_2d_separator(svm, X, eps=.5) # eps 그래프의 확대/축소
custom_mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
sv = svm.support_vectors_
sv_labels = svm.dual_coef_.ravel() > 0
custom_mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
▷ Hyper-parameter(C, gamma)에 따른 결정경계 변화
- C : 데이터 샘플들이 다른 클래스에 놓이는 것을 허용하는 정도
- gamma : 매개변수는 결정 경계의 곡률 조정
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]): # log[-1,0,3] == 0.1, 1, 1000 == C
for a, gamma in zip(ax, range(-1, 2)): # log[-1, 2] == 0.1, 10 == Gamma
custom_mglearn.plot_svm(log_C=C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["Class 0", "Class 1", "Class 0 SupportVector", "Class 1 SupportVector"], ncol=4, loc=(.9, 1.2))
plt.show()
>> 두 값 모두 커질수록 알고리즘의 복잡도 증가, overfitting
실습2) Breast Cancer Datasets
데이터 준비
cancer = load_breast_cancer()train data 75% / test data 25% (default)
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0) 모델 생성, 학습
svc = SVC()
svc.fit(X_train, y_train)
Accuracy
print("Accuracy on Training set: {:.3f}".format(svc.score(X_train, y_train)))
print("Accuracy on Test set: {:.3f}".format(svc.score(X_test, y_test)))
>> train data에 대한 정확도가 100%로 overfitting(과적합) 발생
▷ 과적합의 원인은?
boxplot으로 각 열의 데이터분포 확인
plt.figure(figsize=(10,7))
plt.boxplot(X_train, manage_xticks=False)
plt.yscale("symlog")
plt.xlabel("Feature list")
plt.ylabel("Feature size")
plt.show()
>> 데이터의 각 열마다 다른 scale이 모델에 영향을 주기 때문에 데이터 스케일링(전처리)이 필요함을 알 수 있음
Feature Scaling : 열마다 데이터의 범위가 비슷해지도록 조정
1) Min-max scaling
열마다의 최대가 1, 최소가 0으로 조정
from sklearn.preprocessing import MinMaxScaler
sc_minmax = MinMaxScaler()
sc_minmax.fit(X_train)
X_train_scaled_minmax = sc_minmax.transform(X_train)
X_test_scaled_minmax = sc_minmax.transform(X_test)
## 새로운 input data scaling
# new_data_minmax = sc_minmax.transform(np.array([[1, 2, 3, ... ]])) 
2) Standard scaling
데이터의 평균을 0, 표준편차를 1에 가깝도록 범위 조정
from sklearn.preprocessing import StandardScaler
sc_std = StandardScaler()
sc_std.fit(X_train)
X_train_scaled_std = sc_std.transform(X_train)
X_test_scaled_std = sc_std.transform(X_test)
## 새로운 input data scaling
# new_data_std = sc_std.transform(np.array([[1, 2, 3, ... ]])) 
모델 학습 후 Accuracy 확인
- Min-max scaling
svc = SVC()
svc.fit(X_train_scaled_std, y_train)
print("Accuracy on Training set: {:.3f}".format(svc.score(X_train_scaled_std, y_train)))
print("Accuracy on Test set: {:.3f}".format(svc.score(X_test_scaled_std, y_test)))
- Standard scaling
svc = SVC()
svc.fit(X_train_scaled_std, y_train)
print("Accuracy on Training set: {:.3f}".format(svc.score(X_train_scaled_std, y_train)))
print("Accuracy on Test set: {:.3f}".format(svc.score(X_test_scaled_std, y_test)))
▷ HPO (Hyper Parameter Optimization, 초매개변수 최적화)
Hyper parameter : 모델링 시 사용자가 직접 세팅해주는 값 (*parameter는 학습 과정에서 생성되는 변수)
- Randomized-search 기법
- Grid-search 기법
from sklearn.model_selection import GridSearchCV
# C, gamma 후보 리스트
param_grid = {'C' : [0.1, 1, 10, 100, 1000],
'gamma' : [1, 0.1, 0.01, 0.001, 0.0001],
'kernel' : ['rbf']}
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=1)
# refit : 찾아진 최적의 params로 estimator를 setting할 지 여부
# verbose : 설명의 자세한 정도
grid.fit(X_train_scaled, y_train)
print('The best parameters are ', grid.best_params_)
from sklearn.metrics import classification_report
grid_predictions = grid.predict(X_test_scaled)
print(classification_report(y_test, grid_predictions))
print("Accuracy on Training set: {:.3f}".format(grid.score(X_train_scaled, y_train)))
print("Accuracy on Test set: {:.3f}".format(grid.score(X_test_scaled, y_test)))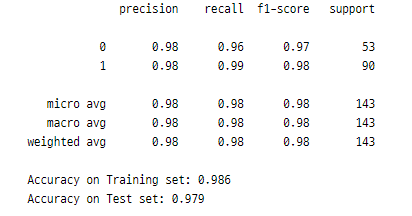
'PYTHON > K-DIGITAL' 카테고리의 다른 글
| [K-DIGITAL] 분류 성능에 대한 측정 ROC Curve와 AUC (0) | 2021.07.01 |
|---|---|
| [K-DIGITAL] 머신러닝 알고리즘(3) 의사결정트리 - sklearn 실습 (0) | 2021.06.30 |
| [K-DIGITAL] 머신러닝 알고리즘(3) 의사결정트리 (0) | 2021.06.30 |
| [K-DIGITAL] 머신러닝 알고리즘(2) SVM (0) | 2021.06.30 |
| [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석(선형, 로지스틱) - sklearn 실습 (0) | 2021.06.29 |
댓글 영역