고정 헤더 영역
상세 컨텐츠
본문
멋쟁이사자처럼 X K-DIGITAL Training - 06.28
[참고] 2021.06.29 - [python/k-digital] - [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석과 분류분석
[K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석과 분류분석
멋쟁이사자처럼 X K-DIGITAL Training - 06.25 지도 학습 (Supervised Learning) 훈련 데이터로부터 하나의 함수를 유추해내기 위한 기계학습 인간 개입에 의한 분석 방법 입력 데이터에 대한 정답인 종속 변
juran-devblog.tistory.com
Scikit-Learn 이용한 LinearRegression 실습
라이브러리
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets, model_selection, linear_model
from sklearn.metrics import mean_squared_errornumpy 행렬 수치 연산 라이브러리
pandas 데이터프레임 생성하여 행과 열의 데이터를 다룰 수 있게 해줌
matplotlib.pyplot 트나 플롯(plot) 그려주는 데이터 시각화 라이브러리
sklearn(사이킷런) 무료 머신러닝 라이브러리
sklearn.datasets 데이터샘플 제공
sklearn.sklearn.linear_model 머신러닝 선형회귀 알고리즘
sklearn.metircs.mean_squered_error MSE 구하는 메서드
데이터 준비
사이킷런에서 제공하는 기본 데이터셋 이용
boston = datasets.load_boston()- boston.target : 주택 가격의 중앙값

- boston.data : 그 외의 요인들
기본 제공 데이터셋 설명
print(boston.DESCR)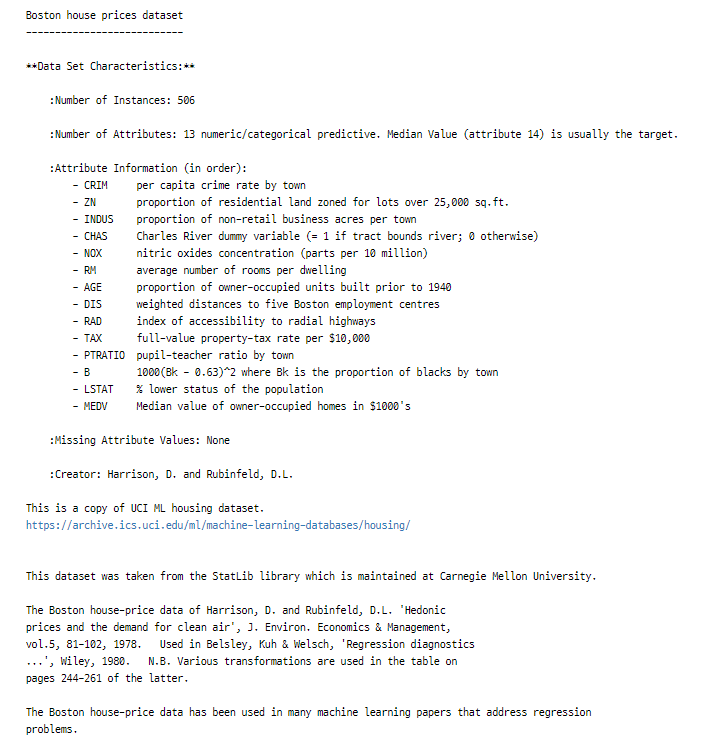
컬럼 설명
0. 범죄율
1. 25,000 평방피트를 초과하는 거주지역 비율
2. 비소매상업지역 면적 비율
3. 찰스강의 경계에 위치한 경우는 1, 아니면 0
4. 일산화질소 농도
5. 주택당 방 수 (거실 외 subroom)
6. 1940년 이전에 건축된 주택의 비율
7. 직업센터의 거리
8. 방사형 고속도로까지의 거리
9. 재산세율
10. 학생/교사 비율
11. 인구 중 흑인 비율
12. 인구 중 하위 계층 비율
타입 확인
type(boston.data)
type(boston.target)>> numpy.ndarray (기본적으로 array 형태로 저장되어있어 바로 활용 가능)
행과 열에대한 정보 확인
boston.data.shape>> (506, 13) 506개의 데이터, 13개의 features
boston.target.shape>> (506, 1) 506개의 라벨값
모델 학습
Feature 선택 - 독립 변수(x), 종속변수(y) 설정
boston_X = boston.data[:, 12:13] # 12. 인구 중 하위 계층 비율
boston_Y = boston.target # 주택 가격Training Data & Test Data 설정
x_train, x_test, y_train, y_test = model_selection.train_test_split(boston_X, boston_Y, test_size=0.3, random_state=0)- test_size : 전체의 30% test data로 지정
- random_state : 랜덤의 패턴 (random_seed, seed)
비어있는 모델 생성 - 선형 회귀분석 모델
model = linear_model.LinearRegression()모델 학습
model.fit(x_train, y_train)>> LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
학습 결과
print('Coefficients: ', model.coef_) # 계수
print('Intercepts: ', model.intercept_) # 교차점>> Coefficients: [[-0.96814078]]
Intercepts: [34.78978059]
→ y = (-0.96814078) * x + 34.78978059
모델 테스트
train 데이터에 대한 예측
model.predict(x_train)- 해당 예측에 대한 MSE
mean_squared_error(model.predict(x_train), y_train)>> 37.93397817288029
test 데이터에 대한 예측
model.predict(x_test)- 해당 예측에 대한 MSE
mean_squared_error(model.predict(x_test), y_test)>> 39.81715050474417
- 제곱근
np.sqrt(mean_squared_error(model.predict(x_test), y_test)) >> 6.310083240714355
→ 선형 회귀의 성능은 그닥 좋지 않음
모델 시각화
plt.figure(figsize=(10, 10))
plt.scatter(x_test, y_test, color="black") # Test data
plt.scatter(x_train, y_train, color="red", s=1) # Train data
plt.plot(x_test, model.predict(x_test), color="blue", linewidth=3) # Fitted line (학습 모델)
plt.show()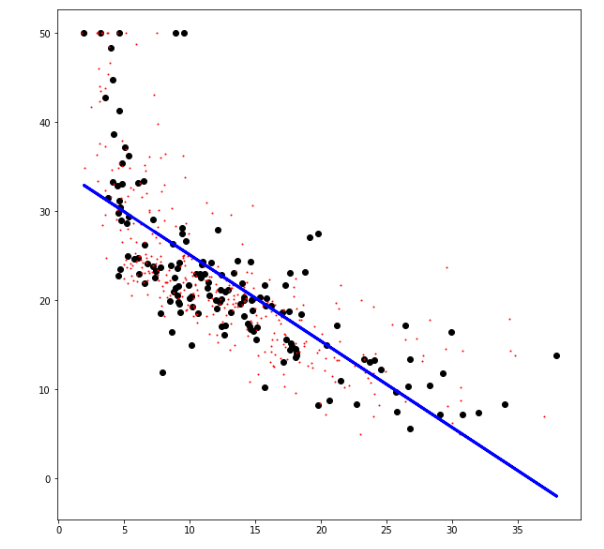
++ 실습추가) Diabetes dataset (당뇨병 진행도 데이터)
# 1. Prepare the data
diabetes = datasets.load_diabetes()
# 2. Feature selection
diabetes_X = diabetes.data[:, 2:3] # BMI(body mass index) 지수
diabetes_Y = diabetes.target
# 3. Train/Test split
x_train, x_test, y_train, y_test = model_selection.train_test_split(diabetes_X, diabetes_Y, test_size=0.3, random_state=0)
# 4. Create model object
model = linear_model.LinearRegression()
# 5. Train the model
model.fit(x_train, y_train)
# 6. Test the model
print('MSE(Training data) : ', mean_squared_error(model.predict(x_train), y_train))
print('MSE(Test data) : ', mean_squared_error(model.predict(x_test), y_test))
# 7. Visualize the model
plt.figure(figsize=(10, 10))
plt.scatter(x_test, y_test, color="black") # Test data
plt.scatter(x_train, y_train, color="red", s=1) # Train data
plt.plot(x_test, model.predict(x_test), color="blue", linewidth=3) # Fitted line
plt.show()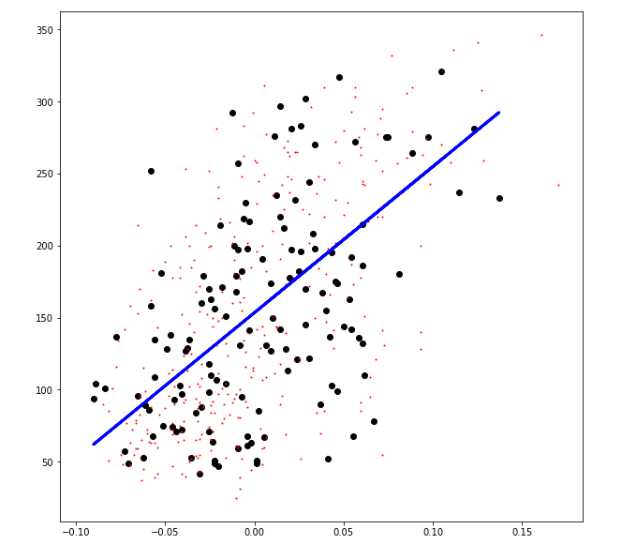
Scikit-Learn 이용한 LogisticRegression 실습
데이터 준비
boston = datasets.load_boston()회귀문제를 분류문제로 바꾸기 위해 새로운 target열 추가
- 평균 주택 가격보다 크면 1, 작거나 같으면 0
# np.array -> dataframe
df_target = pd.DataFrame(boston.target)
# 평균 주택 가격
mean_price = df_target[0].mean()
# 평균 주택가격보다 클때 1, 이하일 때 0
df_target['Label'] = df_target[0].apply(lambda x: 1 if x > mean_price else 0)
boston_Y = np.array(df_target.Label) # y 데이터
boston_X = boston.data # x 데이터
모델 학습
Train data & Test data 설정
x_train, x_test, y_train, y_test = model_selection.train_test_split(boston_X, boston_Y, test_size=0.3, random_state=0)모델 생성 후 학습
model = linear_model.LogisticRegression() # 로지스틱회귀
model.fit(x_train, y_train)
모델 테스트
pred_test = model.predict(x_test)
>> pred_test (예측값)

>> y_test (실제값)

Accuracy
from sklearn.metrics import accuracy_score
print('Accuracy: ', accuracy_score(model.predict(x_test), y_test))>> Accuracy: 0.8552631578947368
모델 시각화
from sklearn.metrics import roc_curve, auc
pred_test_proba = model.predict_proba(x_test)
fpr, tpr, _ = roc_curve(y_true=y_test, y_score=pred_test_proba[:, 1]) # ROC 커브 x축 좌표, y축 좌표
roc_auc = auc(fpr, tpr) >> roc_auc = 0.9118958444801141
plt.figure(figsize=(10, 10))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.title("ROC curve")
plt.show()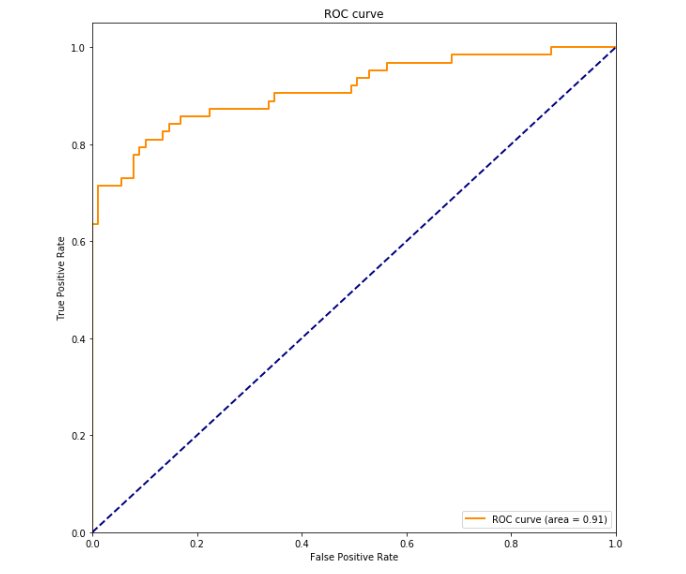
'PYTHON > K-DIGITAL' 카테고리의 다른 글
| [K-DIGITAL] 머신러닝 알고리즘(3) 의사결정트리 (0) | 2021.06.30 |
|---|---|
| [K-DIGITAL] 머신러닝 알고리즘(2) SVM (0) | 2021.06.30 |
| [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석과 분류분석 (0) | 2021.06.29 |
| [K-DIGITAL] 인공지능과 머신러닝 (0) | 2021.06.28 |
| [K-DIGITAL] 파이썬 Selenium으로 크롤링하기(2) + SQLite (0) | 2021.06.28 |
댓글 영역