고정 헤더 영역
상세 컨텐츠
본문
멋쟁이사자처럼 X K-DIGITAL Training - 06.25
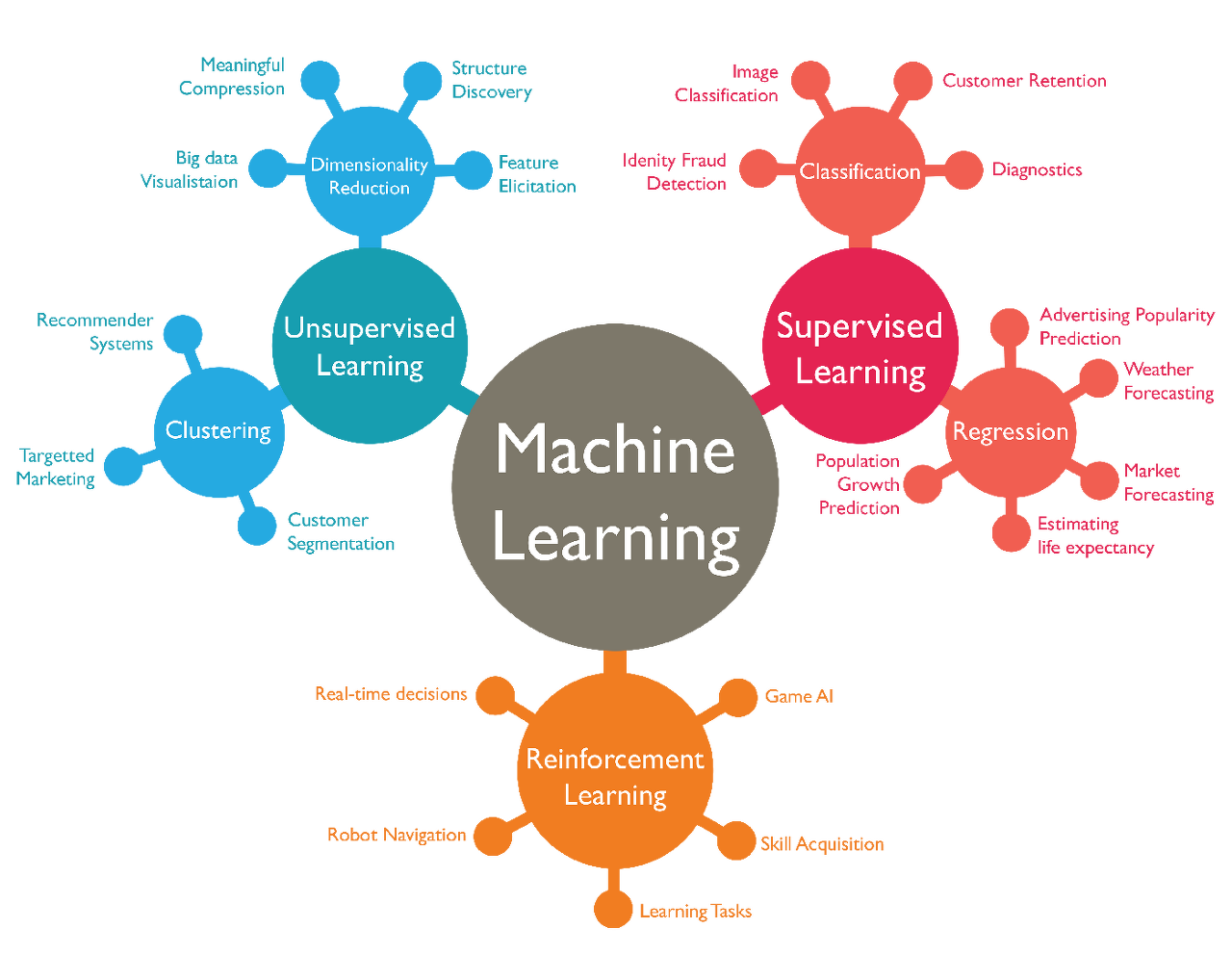
지도 학습 (Supervised Learning)
훈련 데이터로부터 하나의 함수를 유추해내기 위한 기계학습
인간 개입에 의한 분석 방법
입력 데이터에 대한 정답인 종속 변수(y) 존재
지도학습 > 회귀분석
관찰된 연속형 변수들에 대해 두 변수 사이 모형을 구한뒤 적합도를 측정해 내는 분석 방법
독립변인(x)이 종속변인(y)에 영향을 미치는지 알아보고자 할 때 실시하는 분석방법
시간에 따라 변화하는 데이터나 어떤 영향, 가설적 실험, 인과 관계의 모델링등의 통계적 예측에 이용될 수 있다.
Linear Regression (선형 회귀)
종속변수 y와 한개 이상의 독립 변수 x 사이의 선형 상관관계를 모델링하는 회귀분석 기법
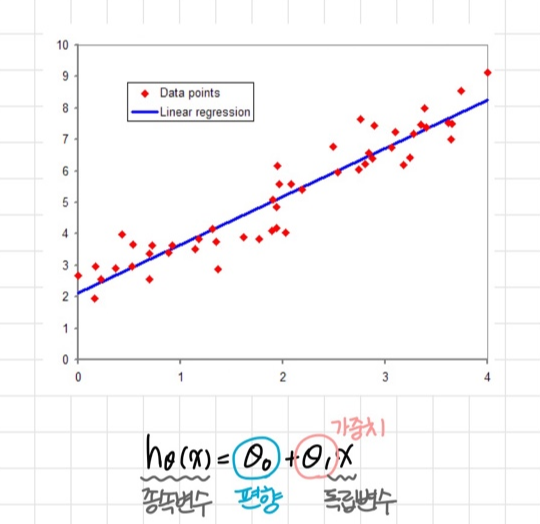
단순 회귀분석 (Simple Regression Analysis)
1개의 독립변수(x)가 1개의 종속변수(y)에 영향을 미칠 때
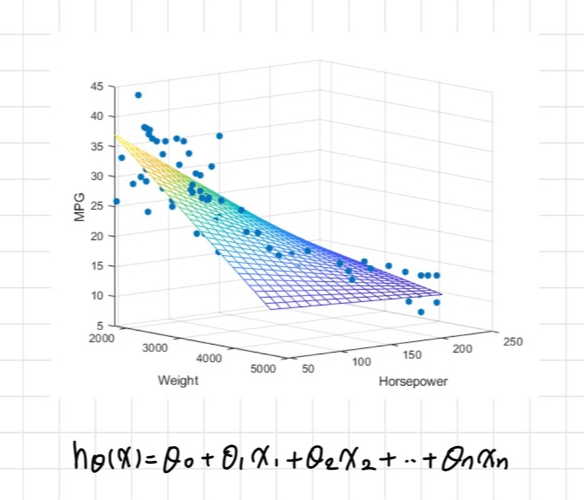
다중 회귀분석 (Multivariate Regression Analysis)
2개 이상의 독립변수(x)가 1개의 종속변수(y)에 영향을 미칠 때
* 가중치의 의미: 클수록 중요하게 여기는 요소(요인)라고 볼 수 있음
→ 가장 적합한 θ(theta)들의 set을 찾는 것이 목표
Cost Function (비용함수, 손실함수)
예측 값과 실제 값의 차이를 기반으로 모델의 성능(정확도)을 판단하기 위한 함수
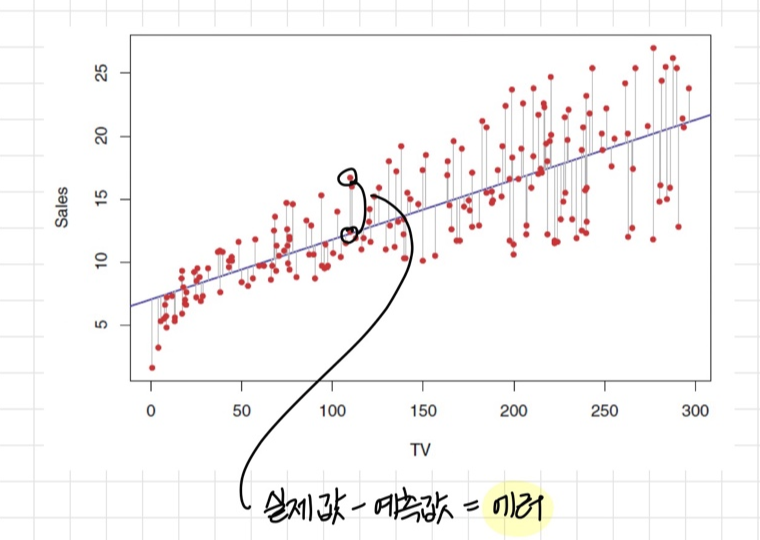
선으로 나타난 그래프는 모델의 예측값이고 점으로 찍힌 값들은 실제 값이며 이 두 값의 차이가 에러
→ 손실함수의 값을 줄이는 것이 예측 모델의 성능을 높히는 것
▷ 선형회귀 비용함수 : MSE(Mean Squere(d) Error Function, 평균 제곱 오차 함수)
(실제 값 - 예측 값)의 제곱들의 평균
MSE(cost)가 최소가 되도록 하는 θ를 찾아야 함
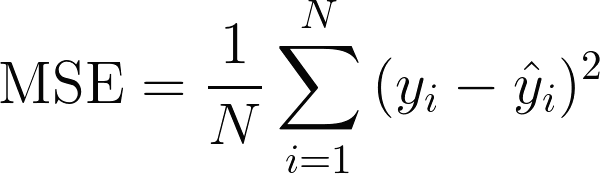
▷ 최적화 알고리즘(옵티마이저) : Gradient Descent Algorithm (경사하강법)
비용함수의 값을 최소로 만드는 θ를 찾아나가는 방법
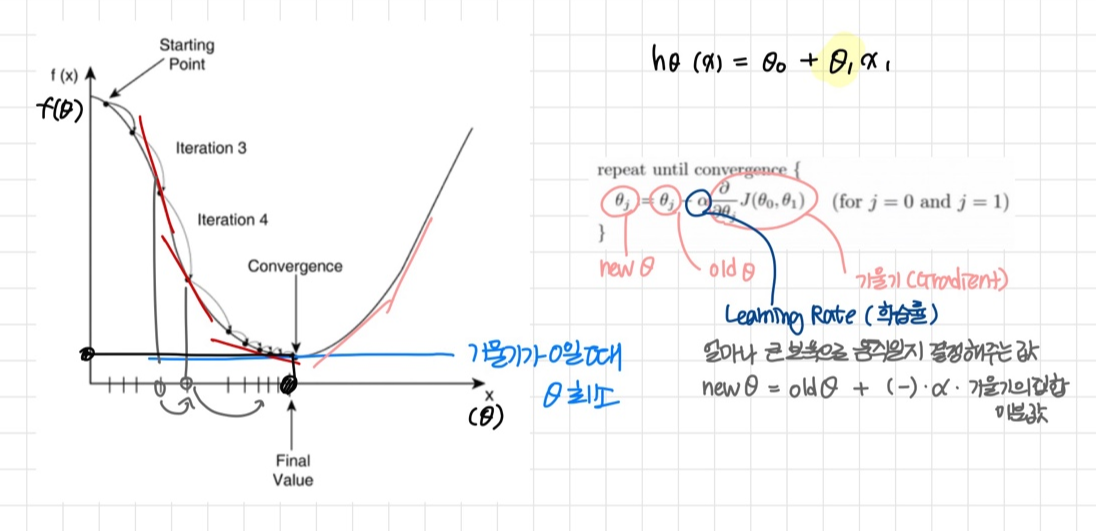
1) 초기 θ값 설정
2) 현재 변수에 대응되는 비용함수의 경사도 계산(미분)
3) 현재 변수에 대응하는 기울기의 반대방향으로 θ 이동
4) 기울기가 0이 될때까지 이동
→ 기울기가 0일때 θ값이 최소
* Learning Rate (학습률)
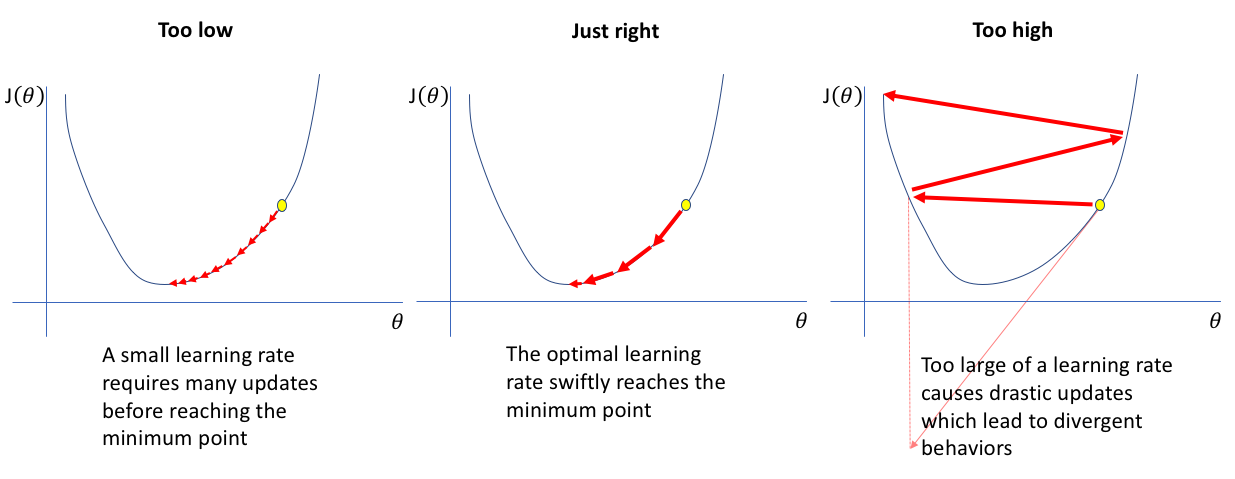
처음 세팅한 값을 갖고 θ 이동시 계속 사용
너무 크면 θ가 최소값에 가지 못하고 튕겨나감으로 작게 잡아주는 것이 좋음
기본적으로 0.01 권장
-> Hyper-Parameter 초매개변수
* Gradient
모든 변수의 편미분을 벡터로 정리한 것, 함수의 기울기
지도학습 > 분류분석
다수의 변수를 갖는 데이터 셋을 대상으로 특정 변수 값을 조건으로 지정하여 데이터를 분류하여 트리 형태의 모델을 생성하는 분석 방법
사전에 정해진 그룹 또는 범주 중의 하나로 분류하여 분석
학습 데이터를 이용하여 분류 모델을 찾은 후 이를 이용하여 새로운 데이터에 대해 분류 값을 예측
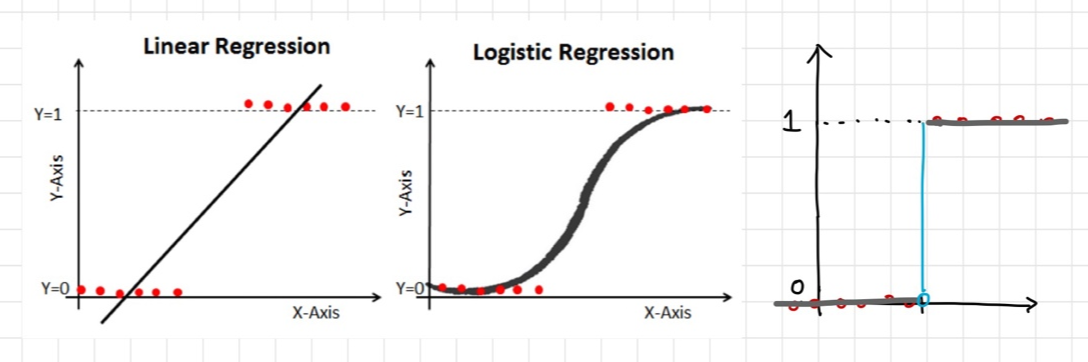
Logistic Regression (로지스틱 회귀)
이진 분류 (binary classificatioin) 문제를 해결하기 위한 모델
회귀를 사용하여 어떤 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 가능성이 더 높은 범주에 속하는 것으로 분류하는 지도학습 알고리즘
예) 스팸 메일 분류, 질병 양성/음성 분류, 신용카드 거래에서 정상 거래 및 이상 거래 분류 등
결과가 나오는 방식
1) [0.32, 0.68] : 각 분류에 속할 확률, 모든 확률의 합은 1
2) 0 또는 1 : 속할 확률이 높은 클래스 반환
▷ Sigmoid Function (시그모이드 함수)
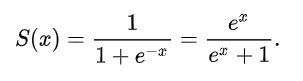
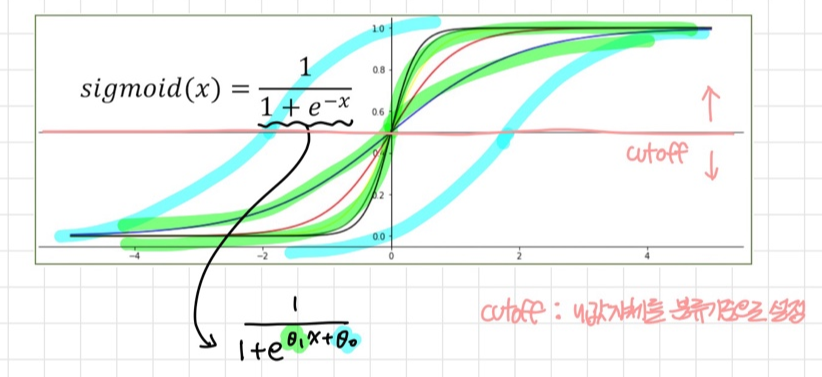
확률을 0과 1사이 부드러운 곡선 그래프 형태로 나타나게 해주는 함수
- log-odds를 sigmoid 함수에 넣어 [0, 1]범위의 확률을 구하거나(x가 class에 속할 확률을 계산하거나)
- sigmoid 함수의 정확한 y값을 이용하여 그 값(cutoff)을 넘는 경우 분류에 대해 예측할 수 있음
▷ 분류분석 비용함수 : Cross-entropy (교차 엔트로피)
* 현재에는 많이 사용하지는 않음
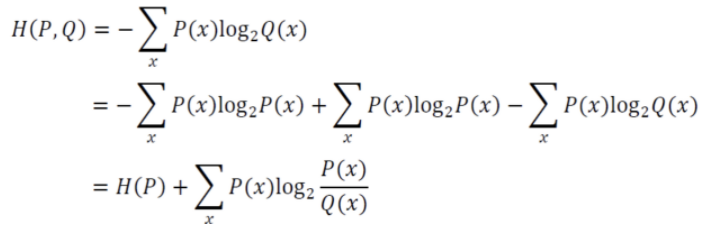
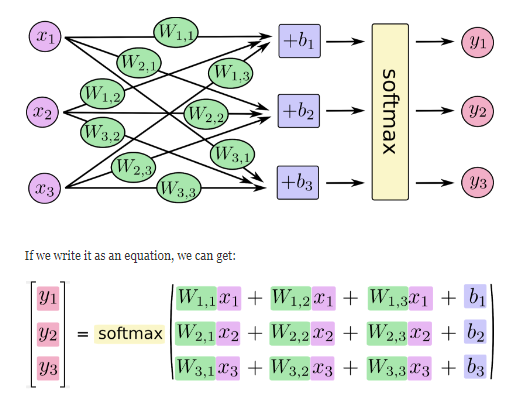
Softmax Algorithm (소프트맥스 알고리즘)
로지스틱 회귀의 확정
다중 클래스 분류 (Multi-class/Multinomial classification) 문제를 위한 알고리즘, 함수
모델의 output에 해당하는 logit을 각 클래스에 소속될 확률로 해당하는 값들의 벡터로 변환하며
입력받은 값의 출력은 0~1 사이 값이고 모든 출력값의 총합은 항상 1
예) 강아지 품종 분류, 필기체 숫자 인식 등
* 멀티 클래스 : 하나의 데이터가 여러 개의 클래스 중 하나의 클래스에 대응
멀티 라벨 : 하나의 데이터가 여러 라벨을 가짐
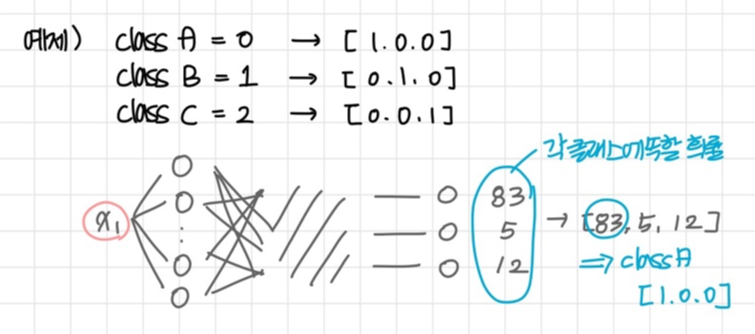
'PYTHON > K-DIGITAL' 카테고리의 다른 글
| [K-DIGITAL] 머신러닝 알고리즘(2) SVM (0) | 2021.06.30 |
|---|---|
| [K-DIGITAL] 머신러닝 알고리즘(1) 회귀분석(선형, 로지스틱) - sklearn 실습 (0) | 2021.06.29 |
| [K-DIGITAL] 인공지능과 머신러닝 (0) | 2021.06.28 |
| [K-DIGITAL] 파이썬 Selenium으로 크롤링하기(2) + SQLite (0) | 2021.06.28 |
| [K-DIGITAL] 파이썬 Selenium으로 크롤링하기(1) (0) | 2021.06.25 |
댓글 영역