고정 헤더 영역
상세 컨텐츠
본문
멋쟁이사자처럼 X K-DIGITAL Training - 06.16
라이브러리
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# font
from matplotlib import font_manager, rc # rc == run configure(configuration file)
%matplotlib inline
font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
rc('font', family=font_name) # run configurepandas 데이터 처리 및 분석 라이브러리로 행과 열로 이루어진 데이터 객체(DataFrame)를 만들어 다룰 수 있음
numpy 벡터, 행렬 등 수치 연산을 수행하는 선형대수 라이브러리
matplotib 데이터를 차트로 시각화
1. 데이터 탐색과 빈도 분석
df = pd.read_csv('data/cosmetics_.csv', encoding = 'utf-8')
df.head()
데이터 - 컬럼 설명
df_col_ex = pd.read_excel('data/cosmetics_데이터 설명_수정.xlsx', encoding = 'utf-8')
df_col_ex.fillna('', inplace=True)
df_col_ex.drop(5, inplace=True) # aware: 인지 브랜드
df_col_ex.drop(['보기11', '보기12', '보기13', '보기14', '보기15', '보기16','보기17', '보기18', '보기19', '보기20', '보기21', '보기22', '보기23', '보기24', '보기25', '보기26', '보기27', '보기28', '보기29', '보기30', '보기31'], axis=1, inplace=True)
df_col_ex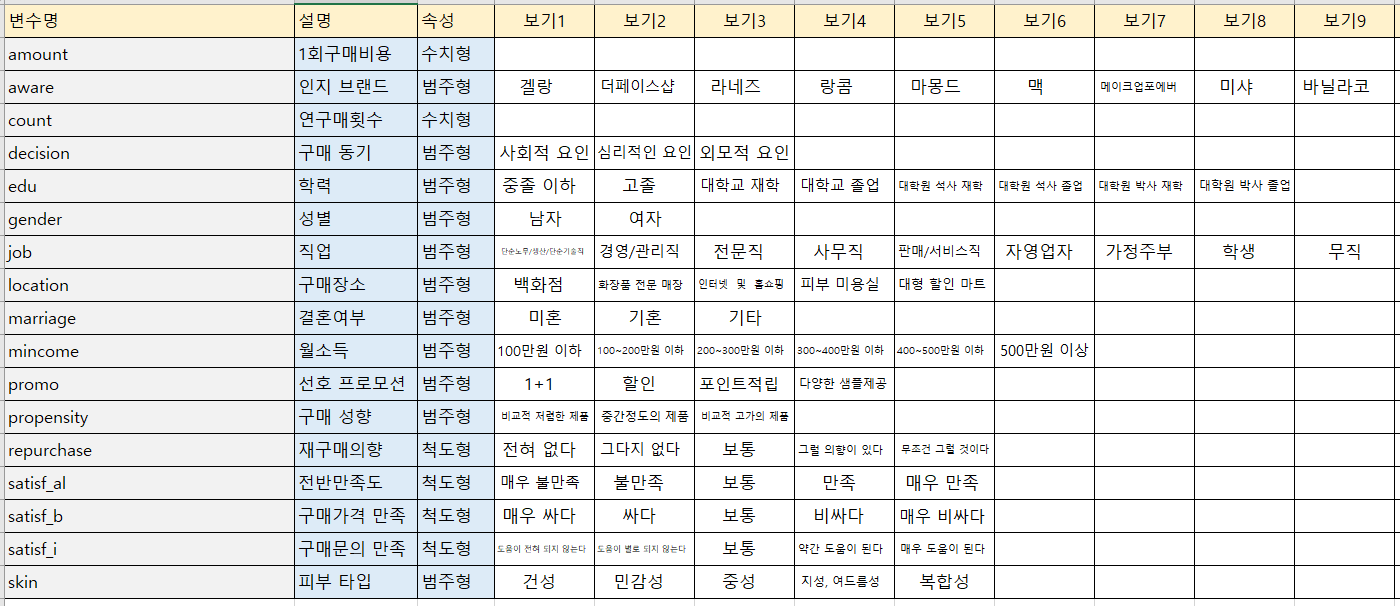
범주형 데이터의 빈도 분석
예시) 'gender'열
# 데이터 변경
df.gender = df.gender.replace([1, 2], ['male', 'female'])각 범주마다 개수 count
df['gender'].value_counts() 
matplot 차트
df.gender.value_counts().plot(kind = 'pie')
2. 데이터 탐색과 기술통계분석
히스토그램
표로 되어있는 도수 분포를 정보 그림으로 나타낸 것 (도수분포표를 그래프로 나타낸 것)
주로 가로축이 계급, 세로축이 도수를 뜻하나 때때로 반대로 그리기도 함 ← 여기서 계급은 보통 변수의 구간을 의미)

왜도(비대칭도) : 분포가 치우처진 정도
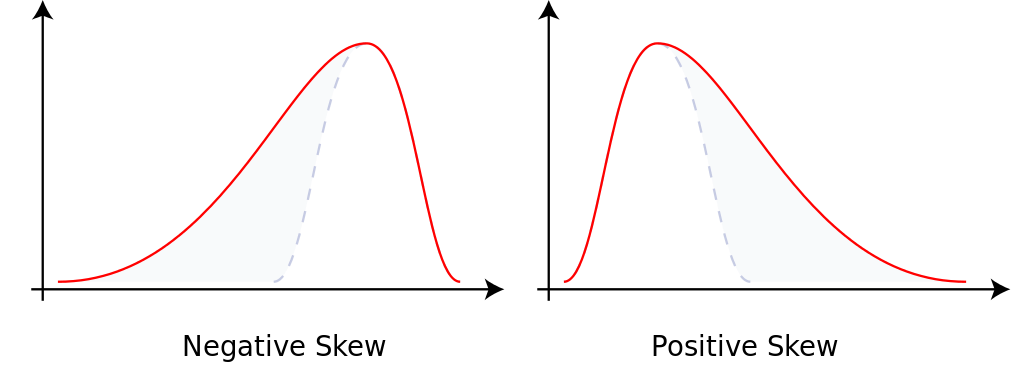
음수일 경우 왼쪽에 긴 꼬리를 가지며 양수일 경우 오른쪽으로 긴 꼬리를 가짐
첨도 : 확률분포의 뾰족한 정도, 관측치들이 어느정도 집중적으로 중심에 몰려있는가 판단

첨도가 클수록 더욱 뾰족한 모양
▷ 왜도가 0, 첨도가 1일때 완전한 정규분포
범주형 변수의 히스토그램
예시) 결혼여부('marriage')열에 대한 히스토그램
# 데이터 변경
df['marriage'] = df['marriage'].replace([1, 2, 3], ['single', 'married', 'other'])범주별 개수 표수
df.marriage.value_counts()
df.marriage.value_counts().plot(kind='bar')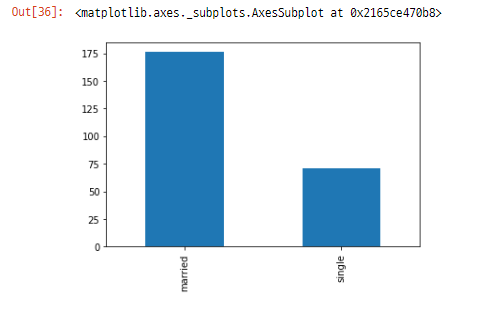
df.marriage.value_counts().hist()
# df.marraige.value_counts().plot(kind='hist')
수치형 변수의 히스토그램
예시) 연 구매 횟수(count)와 1회 평균 구매 비용(amount)을 기준으로 히스토그램 plot
matplotlib
df.amount.hist(bins=50, figsize=(20, 15))
seaborn
- distribution plot(distplot, 히스토그램)
sns.distplot(df.amount, rug=False)
- jointplot(산점도와 히스토그램)
sns.jointplot(x="amount", y="count", data=df)
- kernel - density (kde) : 추정한 확률밀도함수를 겹쳐 그려주는 방법, 히스토그램보다 부드러운 형태의 분포 곡선을 보여줌 (등고선 형태)
sns.jointplot(x="amount", y="count", data=df, kind="kde")
왜도
df.amount.skew()>> 8.727245406515182
df.decision.skew()>> -0.7874015776363626
첨도
df.amount.kurtosis()>> 94.95150601199587
df.job.kurtosis()>> -0.12032961249934582
3. Outlier(이상치) 탐지와 제거
수염상자그림

Median Q2: 중위값(중간값)
Lower Quartile Q1: 하위 25%
Upper Quartile Q3: 상위 25%
Lower Whisker: Q3 - 1.5 * IQR
Upper Whisker: Q3 + 1.5 * IQR
Interquartile Range (IQR) = Q3 - Q1

* quartile / quantile / percentile

예시) 'amount'열
df.amount.quantile() # default 0.5
df.amount.quantile(q=0) # 최소
df.amount.quantile(q=1) # 최대Q2 = df.amount.quantile(q=0.5)
Q1 = df.amount.quantile(q=0.25)
Q3 = df.amount.quantile(q=0.75)
print('Q1 {} / Q2 {} / Q3 {}'.format(Q1, Q2, Q3))>> Q1 30000.0 / Q2 52000.0 / Q3 100000.0
IQR = Q3 - Q1
IQR>> 70000.0
Outlier 기준
- 상한치 : 바닥부터 75% 지점의 값 + IQR의 1.5배 / Q1 (UpperWhisker)
- 하한치 : 바닥부터 25% 지점의 값 - IQR의 1.5배 (Lower Whisker)
기준을 넘으면 Outier로 판단 가능
이상치 데이터프레임
# 이상치
df_outlier = df[ ( (df['amount'] > Q3 + IQR * 1.5) | (df['amount'] < Q1 - IQR * 1.5) )]
# 이상치가 아닌
df_IQR = df[ (df['amount'] < Q3 + IQR * 1.5) & (df['amount'] > Q1 - IQR * 1.5) ]
이상치 제거 전/후 비교
- boxplot
df.boxplot(column='amount')
df_IQR.boxplot(column='amount')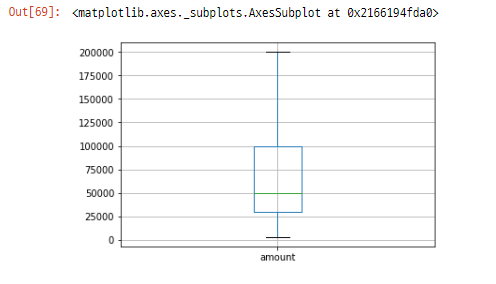
- 히스토그램
df[['amount', 'count']].hist(bins=50, figsize=(20,15))
processed_df = df[['amount', 'count']]
# 상한선에 해당하는 값 제거
processed_df = processed_df[ (processed_df['count'] < 10) & (processed_df['amount'] < 200000) ]
processed_df.hist(bins=50, figsize=(20,15)
- jointplot
sns.jointplot(x="amount", y="count", data=df)
sns.jointplot(x="amount", y="count", data=processed_df)
* Data Scaling
데이터 전처리 과정 중 하나로 데이터 값이 너무 크거나 작은 경우 같은 비율의 다른 값으로 처리해주는 과정
1) standard scaling: 평균 0, 분산 1로 변경 (대게 min-max보다 더 나은 성능)
2) robust scaling: 평균과 분산 대신 median과 quartile 사용, 이상치에 영향을 받지 않음
3) min-max scaling: 모든 값이 0과 1 사이 위치 (경우에 따라 다르지만 데이터가 많을 때 성능이 그렇게 좋지는 않음)
4) max-abs scaling: 각 특성의 절대값이 0과 1사이 되도록 (-1 ~ 1)
5) normalizer: 행마다 각각 정규화, 유클리드 거리가 1이 되도록 데이터 조정(유클리드 거리는 두 점 사이 거리를 계산할 때 쓰는 방법)
예시)
processed_df.head()
스케일링 전
sns.jointplot(x="amount", y="count", data=processed_df, kind="kde")
>> count에 비해 amount의 scale이 너무 큰 상태
스케일링 후
processed_df.amount = np.log(processed_df.amount)
sns.jointplot(x="amount", y="count", data=processed_df, kind="kde")
'PYTHON > K-DIGITAL' 카테고리의 다른 글
| [K-DIGITAL] 세미프로젝트1. 서울시 자전거사고 분석(3) 상관관계 (0) | 2021.06.22 |
|---|---|
| [K-DIGITAL] 파이썬을 활용한 기초 통계분석(2) 상관관계 (0) | 2021.06.22 |
| [K-DIGITAL] 세미프로젝트1. 서울시 자전거사고 분석(2) 원인예측 (0) | 2021.06.19 |
| [K-DIGITAL] 세미프로젝트1. 서울시 자전거사고 분석(1) 문제분석 (0) | 2021.06.18 |
| [K-DIGITAL] 파이썬 통계자료 분석 및 시각화(2) 데이터 시각화 (0) | 2021.06.16 |
댓글 영역